Introducción Práctica a Deep Learning (Taller 1)

Nota: aquí están los slides, el código parte 1 y parte 2, y el video de Facebook live del taller.

Durante las vacaciones de fin de año tuve la oportunidad de viajar a mi país y llevar a cabo dos talleres de inteligencia artificial con la comunidad de Data Science El Salvador. En el primer taller cubrimos redes neuronales desde cero teórica y prácticamente utilizando Python y la librería NumPy. En el segundo, nos enfocamos en PyTorch, uno de los frameworks más populares para deep learning. El taller despertó bastante interés en la comunidad , incluyendo la participación de estudiantes de la UCA y la UES, compañías como SPOT, Applaudo Studios, y Avianca, e incluso miembros de otras comunidades de desarrollo de software como HorchataJS! Gracias a todos por asistir! Y especiales gracias a Ricardo Ríos por organizar el evento!

Este post cubre la implementación de redes neuronales desde cero incluyendo un poco de teoría. Específicamente:

Introducción al perceptron
Función de error
Gradiente descendente
Redes neuronales
Propagación del error (backpropagation)
Implementación

Para entrenar y evaluar el modelo, vamos a utilizar dos datasets:

Moons dataset (sección 7): el dataset de lunas
MNIST dataset (sección 8): el dataset de reconocimiento de dígitos escritos a mano

1. Introducción al perceptron

Las redes neuronales artificiales están inspiradas en las redes neuronales humanas. El principal concepto detrás es el perceptron, que escencialmente representa una neurona. Los componentes de un perceptron son las señales de entrada, la transformación lineal, la activación, y la salida.

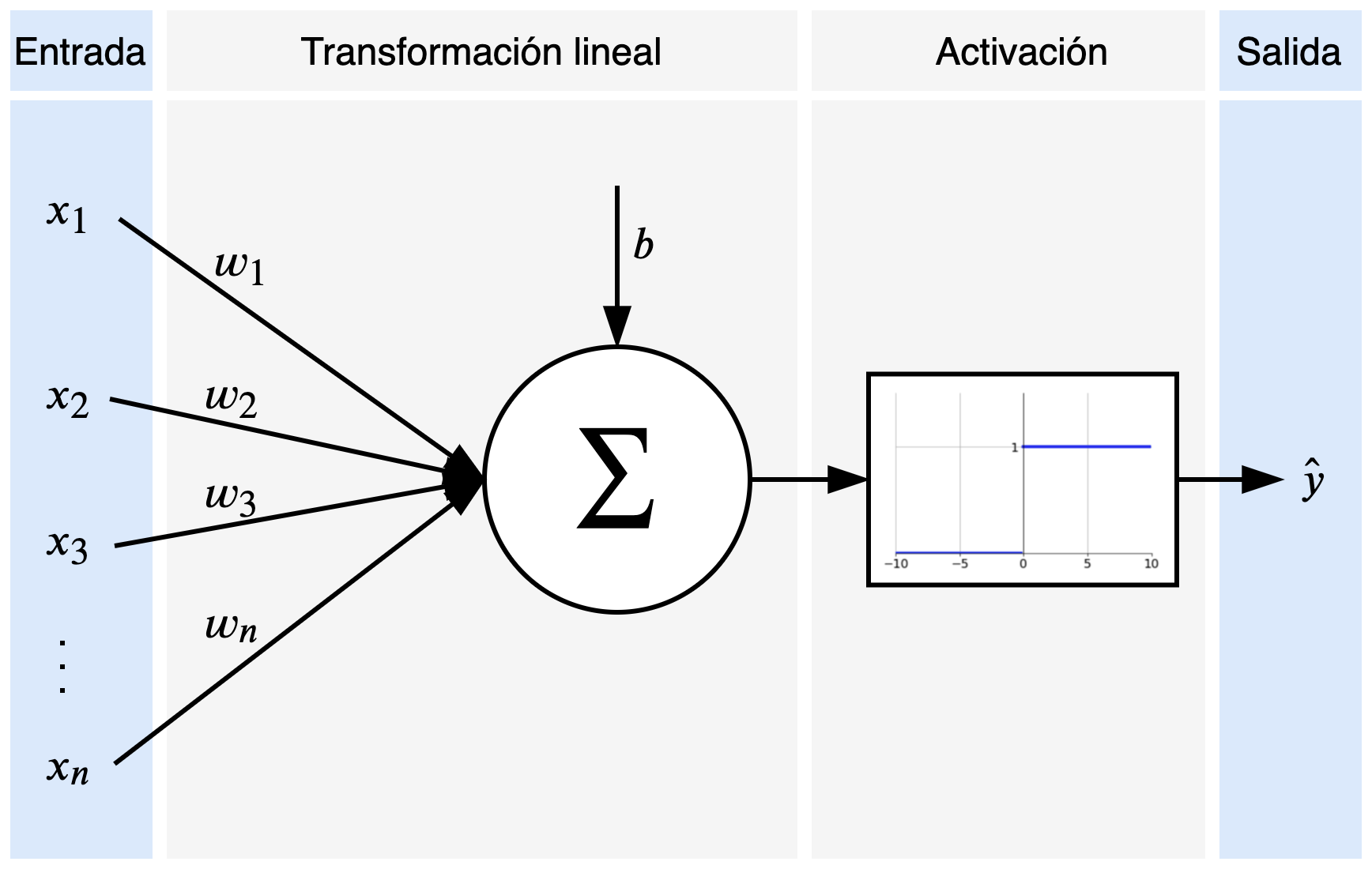
En la Figura 1 se pueden observar las entradas $x_1, x_2, \dots, x_n$ y la salida $\hat{y}$ en los bloques azules. Si consideramos el ejemplo de otorgamientos de préstamos, las entradas podrían ser datos del cliente como la edad, el salario, tiempo trabajando continuamente, etc. Mientras que la salida sería si se le otorga el préstamo al cliente o no. La decisión de entregar o no el préstamo la determina la función de activación, que en este caso es la función escalón unitario (genera cero si el préstamo es rechazado o uno si es otorgado). Para poder decidir sobre el préstamo, el modelo utiliza los parámetros $\theta = \{w_1, w_2, w_3, \dots, w_n, b\}$. Estos parámetros son pesos que determinan lo relevante que son cada uno de los elementos de entrada (por ejemplo, el salario del cliente es más importante que su estado civil). Los componentes del perceptron pueden escribirse de la siguiente manera:

\[\begin{aligned} \hat{y} =& ~g(w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b) \\\\ & ~g(x) = \begin{cases} 0 ~~~~\mathrm{si} ~~x < 0, \\ 1 ~~~~\mathrm{si} ~~x \ge 0 \end{cases} \end{aligned}\]

Con este simple modelo podríamos predecir si una persona es apta para un préstamo o no, y la calidad de nuestro modelo depende de los parámetros que tenga.

¿Cómo encuentro los parámetros adecuados?

Si pensamos en valores aleatorios para cada uno de los parámetros $w$’s, estaríamos otorgando préstamos a clientes sin importar sus condiciones y características. Sin embargo, con esos valores iniciales podemos determinar qué tan malo es el modelo, y a partir de ahí podemos mejorarlo.

Para mejorarlo tenemos que cuantificar el error asociado al modelo, y minimizarlo. Esto nos lleva a definir una función de error.

2. Función de error

El siguiente diagrama muestra dos modelos que discriminan cuatro puntos. El modelo de la izquierda classifica erróneamente dos puntos (los puntos $s_2$ y $s_3$), mientras que el de la derecha clasifica correctamente los cuatro puntos. Este simple conteo nos dice que el modelo de la derecha es mejor que el de la izquierda. El problema ahora es que al intentar una línea diferente puede que sigamos teniendo los mismos dos errores, y no sabríamos si nos estamos acercando al modelo de la derecha o no.

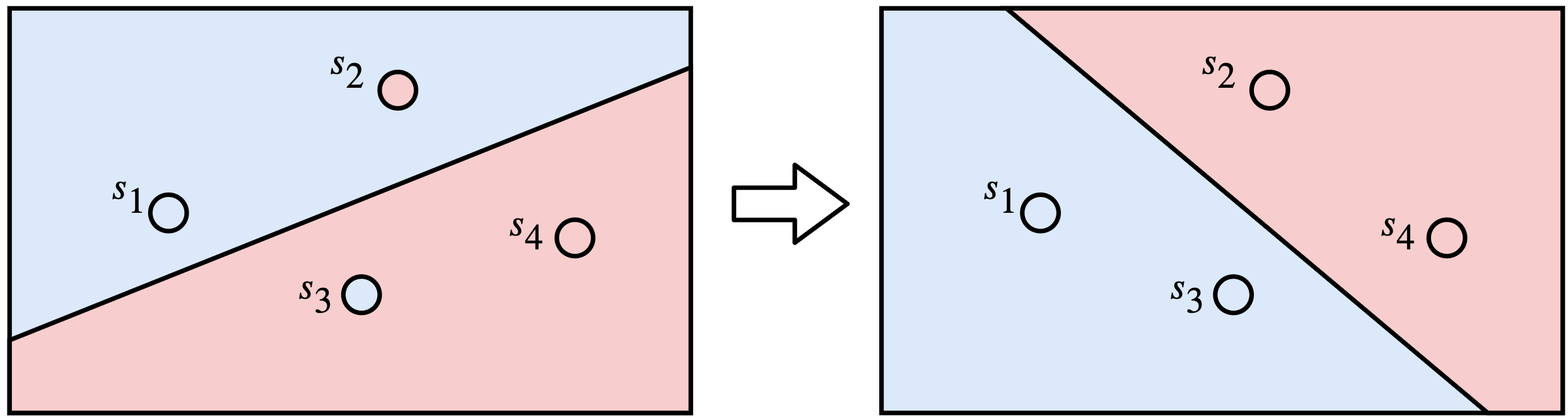
Fig. 2 - Modelo con parámetros iniciales (izquierda) y parámetros ideales (derecha).

Nuestro principal problema es que el perceptron produce valores discretos (ceros o unos a partir de la función escalón unitario) y para monitorear que cada movimiento de la línea es una mejora necesitamos valores continuos. ¿Qué tal si solo utilizamos la transformación lineal sin pasar a la función de activación? El problema es que podemos tener tanto valores negativos como positivos por cada punto, y esto no permite la simple suma de los errores.

Además, nos interesa saber qué tan probable es un punto de recibir cierta clase (por ejemplo, un cliente de recibir un préstamo). Por lo tanto, necesitamos hacer los siguientes cambios:

Modificar la función de activación discreta a continua
Generar valores de salida en un espacio de probabilidad

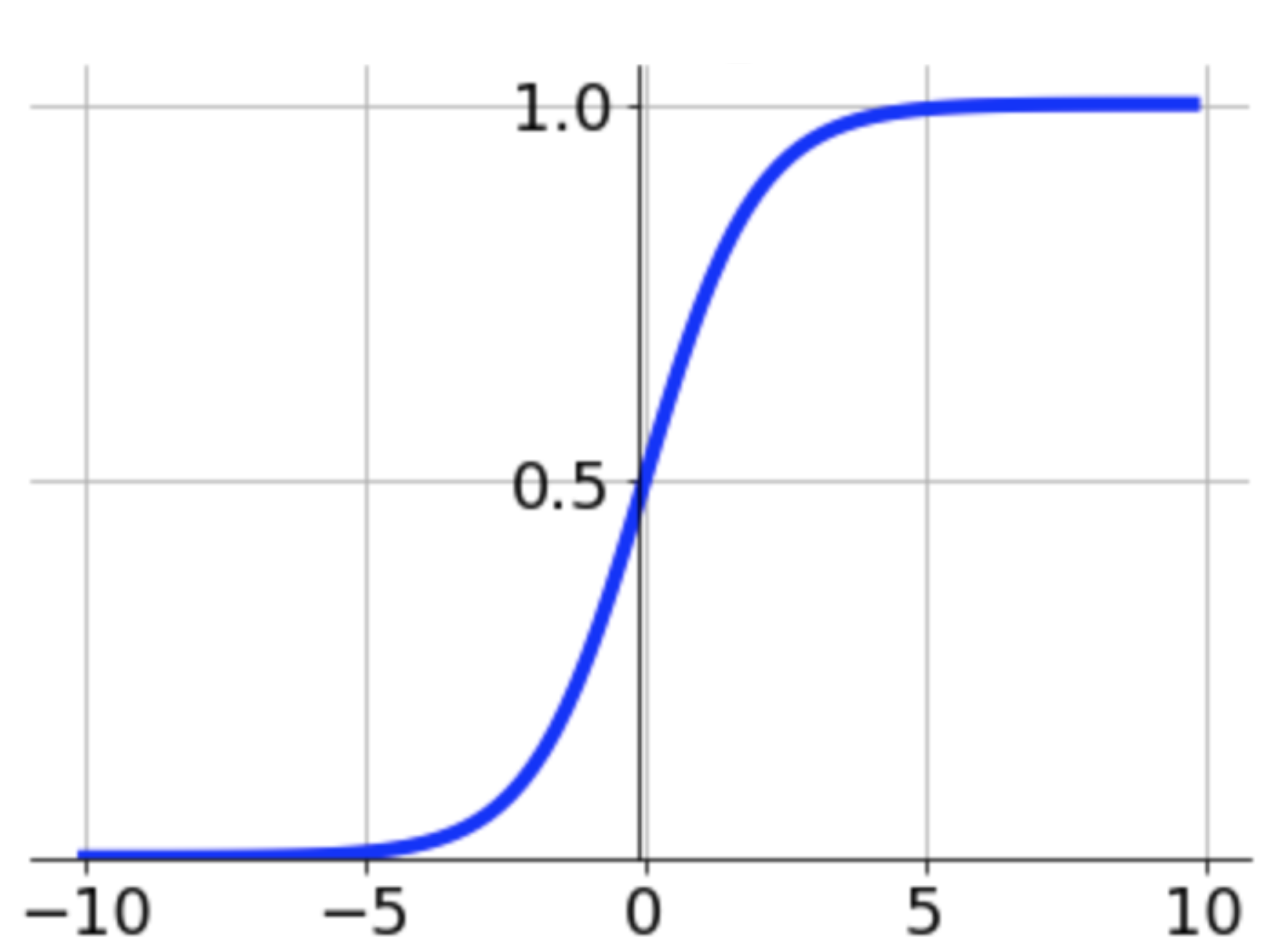
Para ello vamos a utilizar la función sigmoid:

Esta función toma cualquier valor y lo proyecta en un espacio continuo entre 0 y 1 (un espacio de probabilidad). Además, la función intercepta en 0.5 cuando el valor de entrada es 0, lo que permite definir equilibradamente si el modelo escoge una clase u otra como la clase más probable:

\[decision(z) = \begin{cases} 0 ~~~~\mathrm{si} ~~\sigma(z) < 0.5, \\ 1 ~~~~\mathrm{si} ~~\sigma(z) \ge 0.5 \end{cases}\]

Estimación de la Probabilidad Máxima (MLE)

Ahora que el modelo produce valores continuos podemos mejorar la línea de clasificación maximizando las probabilidades. Como nos interesa clasificar varios puntos correctamente y a la vez producir un solo valor para evaluar el modelo, vamos a calcular la probabilidad conjunta de todos los puntos considerando cada punto como un evento independiente condicionado a los parámetros $\theta$ del modelo:

\[\begin{aligned} \mathrm{P}(s_1, s_2, \dots, s_n) &= ~\prod_{i=1}^N ~\mathrm{P}(s_i |~\theta) \end{aligned}\]

Sin embargo, multiplicar tantas probabilidades reduciría rápidamente la resolución del resultado, y muy probablemente generaría error de “underflow”. En lugar de multiplicar usaremos sumas con ayuda de logaritmos:

\[\begin{aligned} \mathrm{P}(s_1, s_2, \dots, s_n) &= ~\prod_{i=1}^N ~\mathrm{P}(s_i |~ \theta) \\ &= ~log~\prod_{i=1}^N ~\mathrm{P}(s_i |~\theta) \\ &= ~log~\mathrm{P}(s_1|~\theta) + log~\mathrm{P}(s_2|~\theta) + \dots + log~\mathrm{P}(s_n|~\theta) \\ &= ~\sum_{i=1}^N log~\mathrm{P}(s_i|~\theta) \\ \end{aligned}\]

Esta fórmula nos ayuda a maximizar el modelo. Sin embargo, en deep learning utilizamos el algoritmo “gradiente descendente” para optimizar nuestros modelos a partir de minimizar una función de error. Por tanto, en lugar de maximizar nuestra fórmula, vamos a minizarla haciendo negativa la expresión anterior:

$$ \begin{aligned} \operatorname*{argmin}_{\theta} ~-\sum_{i=1}^N log~\mathrm{P}(s_i |~\theta) \\ \end{aligned} $$

A esta fórmula se le conoce como “cross-entropy” o “negative log-likelihood”, y también se utiliza bastante en “information gain”.

Pero… ¿por qué estamos minimizando algo con signo negativo?

Si graficamos la función negativa del logaritmo obtenemos la curva de la Figura 4. Recuerda que estamos sacando el logaritmo de probabilidades, así que nuestros $x$’s están en el dominio de 0 a 1 (parte roja). Nota que cuando la función negativa del logaritmo recibe la máxima probabilidad (es decir, 1), el valor que genera es 0. Esto es equivalente a decir no hay ningún error porque el modelo está 100% seguro de la predicción. Opuestamente, si el modelo está, por ejemplo, 20% seguro, el error va a ser mayor a cero, y significa que el modelo aún tiene que mejorar. En pocas palabras, al maximizar las probabilidades también estamos minimizando el error, que es lo que nos interesa para optimizar el modelo.

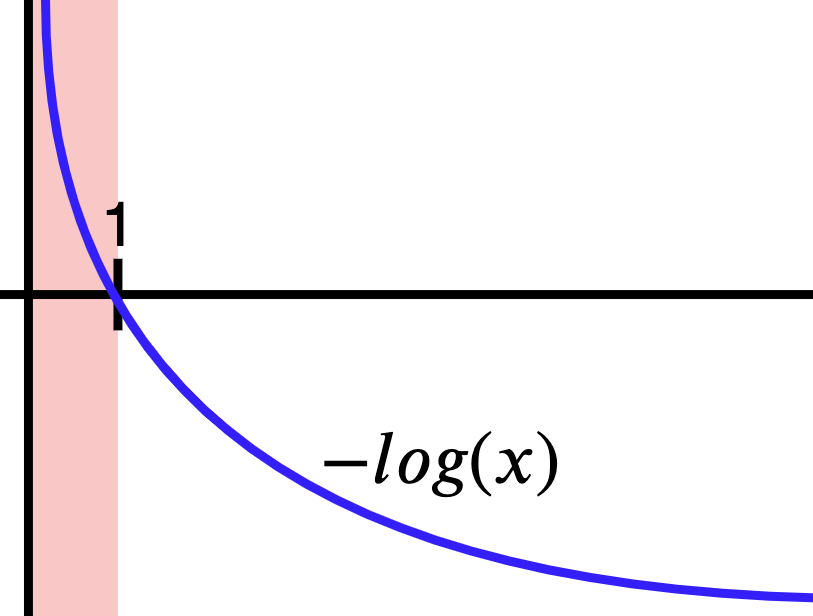
Función de error para clasificación binaria

Hasta ahora la función de error nos dice el error de cada clase. Por ejemplo, el error tanto de otorgar un préstamo a un cliente como también el error de rechazarlo. Sin embargo, cuando corregimos a nuestro modelo solo vamos a corregirlo de acuerdo a la decisión que debía haber tomado. Si el modelo tenía que haber rechazado el préstamo, entonces solo utilizamos ese error e ignoramos el error de otorgar el préstamo.

Asumamos que aceptar el préstamo está representado por el número 1; y rechazarlo, por el 0. Nuestro valor real (lo que esperaríamos que el modelo aprenda) es $y_i$ y la probabilidad de predecir la clase $y_i$ está dada por $p_i$:

$$ \mathcal{L}_{ce} = - \frac{1}{N} \sum_{i=1}^{N} y_i log(p_i) + (1-y_i) log(1 - p_i) $$

Nota que por cada ejemplo $i$ la expresión anterior cancela uno de sus dos términos dependiendo del valor de $y_i$. Si $y_i = 0$ (e.g., rechazar el préstamo), se cancela el término de la izquierda y se usa el de la derecha, y viceversa.

3. Gradiente descendente

Ya tenemos el modelo con sus parámetros y la función de error. Ahora necesitamos optimizar el modelo, y para ello vamos a utilizar el gradiente descendente. Los pasos del algoritmo son los siguientes:

Generar las predicciones $\hat{y}$ a partir de los parámetros actuales del modelo:
\[\hat{y} = \sigma(w_1 x_1 + \dots + w_n x_n + b)\]
Calcular el error de las predicciones:
\[\mathcal{L} = - \frac{1}{N} \sum_{i=1}^{N} y_i log(\hat{y}_i) + (1-y_i) log(1 - \hat{y}_i)\]
Calcular el gradiente o error asociado a cada uno de los parámetros del modelo por medio de derivadas parciales:
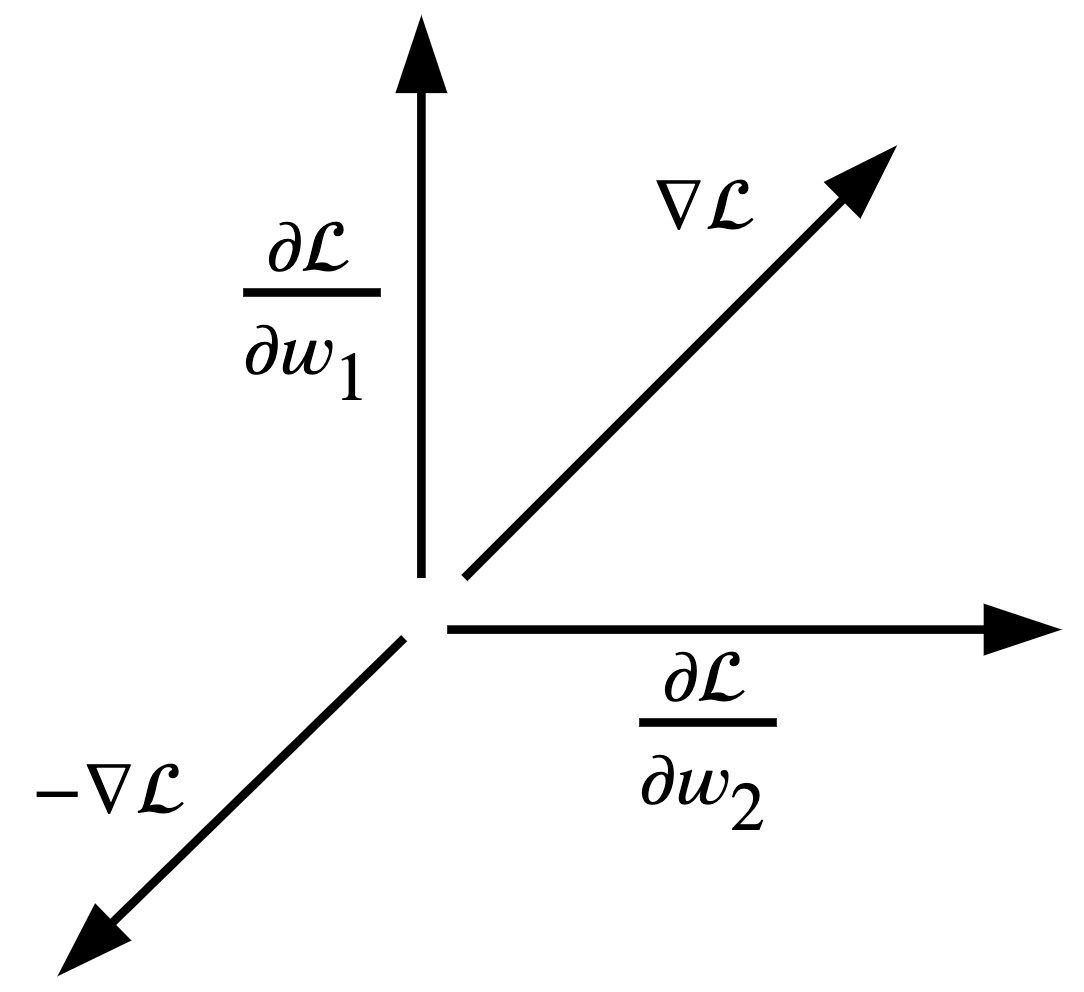
\[\nabla \mathcal{L} = (\frac{\partial \mathcal{L}}{\partial w_1}, \dots, \frac{\partial \mathcal{L}}{\partial w_n}, \frac{\partial \mathcal{L}}{\partial b})\]
Actualizar los parámetros utilizando el gradiente:
\[w_i \leftarrow w_i - \alpha \frac{\partial \mathcal{L}}{\partial w_i}; ~~~ b \leftarrow b - \alpha \frac{\partial \mathcal{L}}{\partial b}\]
Volver al paso 1 con mejores predicciones que la iteración actual.

Algunos detalles importantes son que en el paso 1 asumimos parámetros aleatorios como punto de partida. En el paso 4 utilizamos $\alpha$ como el radio de aprendizaje (“learning rate”). La idea de $\alpha$ es que podamos optimizar el modelo más establemente, asegurándonos de converger en el mínimo local del error. Un $\alpha$ muy grande haría modificaciones severas en los parámetros, y nos llevaría a diverger de la solución que buscamos.

Cabe resaltar que en el paso 4 restamos el delta de modificación (el error multiplicado por el radio de aprendizaje) al parámetro actual. Esto se debe a que estamos minimizando el gradiente, no maximizándolo, y por tanto debemos usar la dirección opuesta:

Fig. 5 - Dirección opuesta del gradiente.

4. Redes neuronales

Hasta aquí nuestro modelo es un simple perceptron con limitada capacidad de abstracción. Sin embargo, el perceptron es el componente básico de una red neuronal artificial, compuesta de muchos perceptrons. La forma en la que varios perceptrons actuan conjuntamente es utilizando la salida de uno como la entrada de otro. A la composición de perceptrons se les llama multi-layer perceptron (MLP), que es equivalente a una red neuronal.

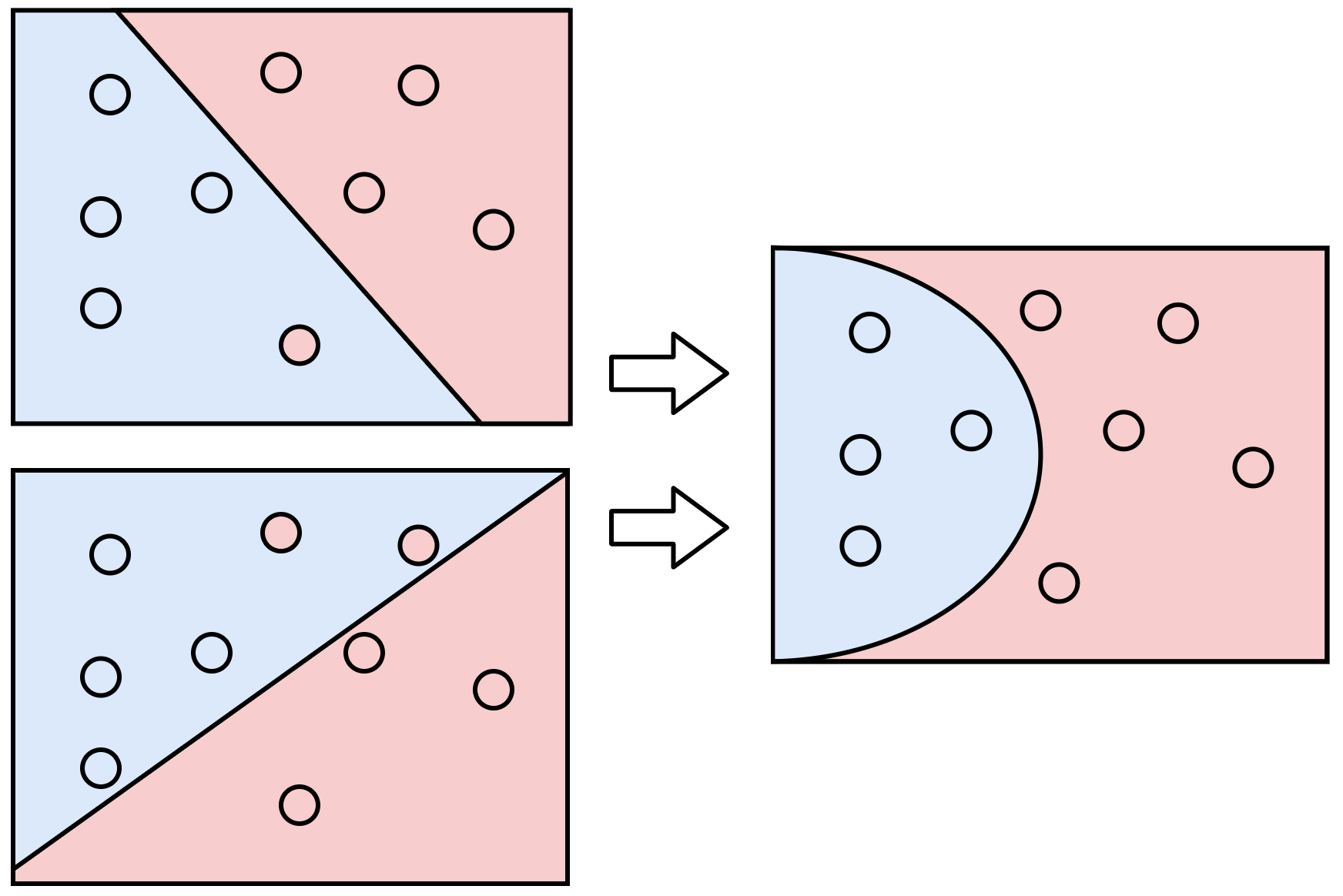
Fig. 6 - Combinación de modelos para incrementar complejidad.

En la Figura 6 vemos que al combinar dos modelos simples (lado izquierdo) podemos mejorar la capacidad de abstracción del modelo de la derecha. De hecho, podríamos agregar pesos a cada modelo simple y decir que queremos priorizar más un modelo que otro con el fin de mejorar el modelo final. En esencia, esto es equivalente a generar otro perceptron que recibe las salidas de los modelos previos. Las redes neuronales son precisamente eso, combinación de varios perceptrons.

Veamos la siguiente red neuronal:

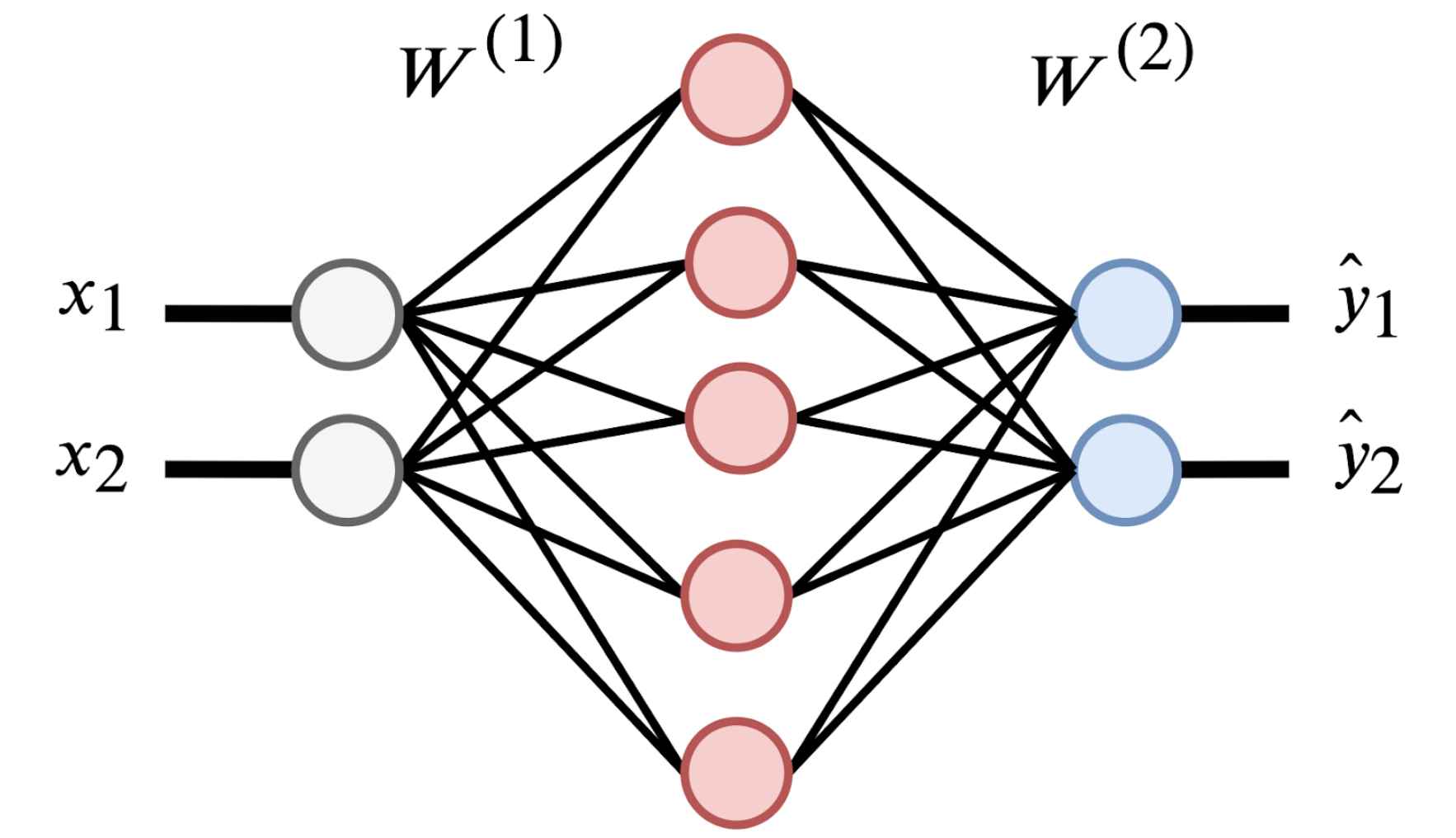
Fig. 7 - Multi-later perceptron de dos capas.

Esta red neuronal tiene dos entradas $x_1, x_2$ (círculos grises) y dos capas neuronales. La primera capa es de cinco neuronas (círculos rojos) y la segunda es de dos neuronas (círculos azules). La primera capa puede variar en la cantidad de neuronas, pero la segunda se define a partir del número de clases posibles (por ejemplo, para predecir dígitos usaríamos 10 neuronas). Nota que cada una de las neuronas es equivalente al perceptron que definimos anteriormente, y por tanto, cada conexión de la figura representa un parámetro o peso de la red.

NOTA: en el caso de clasificación binaria podríamos utilizar una sola neurona, pero por practicidad y generalización a múltiple clases vamos a usar tantas neuronas como clases sean.

Los parámetros de la Figura 7 están representados por las matrices $\mathrm{W}_{1}$ y $\mathrm{W}_{2}$, cuyos índices se refieren a la capa a la que pertenecen. Hay que tomar en cuenta que los interceptos $b_{1}$ y $b_{2}$ están omitidos por simplicidad, pero también son parte del modelo. Así es como se verían las matrices de parámetros:

\[\mathrm{W}_{1} = \begin{bmatrix} w_{1,1} & w_{1,2} & w_{1,3} & w_{1,4} & w_{1,5}\\ w_{2,1} & w_{2,2} & w_{2,3} & w_{2,4} & w_{2,5} \end{bmatrix}_{2 \times 5} ~~~~~ \mathrm{W}_{2} = \begin{bmatrix} w_{1,1} & w_{1,2} \\ w_{2,1} & w_{2,2} \\ w_{3,1} & w_{3,2} \\ w_{4,1} & w_{4,2} \\ w_{5,1} & w_{5,2} \\ \end{bmatrix}_{5 \times 2}\]

En notación de matrices, nuestra red neuronal podría escribirse de la siguiente forma:

\[\begin{aligned} z_1 &= x~\mathrm{W}_1 + b_1 \\ a_1 &= \sigma(z_1) \\ \\ z_2 &= a_{1} \mathrm{W}_{2} + b_{2} \\ \hat{y} &= a_2 = \sigma(z_2) \end{aligned}\]

Aquí tanto $x$ como $\hat{y}$ son matrices de la forma $n \times 2$, siendo $n$ el número de ejemplos.

5. Propagación del error (“Backpropagation”)

Optimizar la red neuronal es un poco más complicado que optimizar un solo perceptron. Sin embargo, ocupamos el mismo principio de asociar parte del error global $\mathcal{L}$ a cada uno de los parámetros. La diferencia con el perceptron es que en la red neuronal tenemos funciones de funciones. Por tanto, necesitamos aplicar la regla de la cadena para obtener el delta del error que generó cada parámetro, incluyendo los parámetros de la capa incial.

Nuestro objetivo es encontrar las derivadas parciales del error con respecto a los parámetros $\mathrm{W}_2, b_2, \mathrm{W}_1, b_1$:

\[\begin{aligned} \nabla \mathcal{L} = ( \frac{\partial \mathcal{L}}{\partial \mathrm{W}_2}, \frac{\partial \mathcal{L}}{\partial b_2}, \frac{\partial \mathcal{L}}{\partial \mathrm{W}_1}, \frac{\partial \mathcal{L}}{\partial b_1} ) \end{aligned}\]

Aplicando la regla de la cadena para los parámetros $W_1, W_2$, tendríamos las siguientes expresiones:

\[\begin{aligned} \frac{\partial \mathcal{L}}{\partial \mathrm{W}_2} &= \frac{\partial \mathcal{L}}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z_2} \frac{\partial z_2}{\partial \mathrm{W}_2} \\ \frac{\partial \mathcal{L}}{\partial \mathrm{W}_1} &= \frac{\partial \mathcal{L}}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z_2} \frac{\partial z_2}{\partial a_1} \frac{\partial a_1}{\partial z_1} \frac{\partial z_1}{\partial \mathrm{W}_1} \\ \end{aligned}\]

El cálculo de las derivadas para cada uno de los parámetros lo colocaré aquí (enlace pendiente). Por ahora solo utilizaremos las soluciones directamente.

$$ \begin{aligned} \delta_3 = \frac{\partial \mathcal{L}}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z_2} &= \hat{y} - y \\ \frac{\partial \mathcal{L}}{\partial \mathrm{W}_2} &= a_1^{\intercal} \delta_3 \\ \frac{\partial \mathcal{L}}{\partial b_2} &= 1^{\intercal} \delta_3 \\ \\ \delta_2 = \delta_3 \mathrm{W}_2^{\intercal} * & \sigma'(z_1) \\ \frac{\partial \mathcal{L}}{\partial \mathrm{W}_1} &= a_0^{\intercal}\delta_2 = x^{\intercal}\delta_2 \\ \frac{\partial \mathcal{L}}{\partial b_1} &= 1^{\intercal} \delta_2 \end{aligned} $$

Ahora que tenemos las derivadas parciales podemos seguir el mismo procedimiento del gradiente descendente.

6. Implementación

Finalmente hemos llegado a la parte divertida del post! Felicidades por leer hasta aquí! Ahora vamos a implementar el mismo modelo de la Figura 7.

El plan de la implementación va así:

Declaración de parámetros. Haremos una clase en Python que contenga los parámetros y los inicialice con valores aleatorios en el constructor.
Forward pass. Agregaremos un método a la clase para generar las predicciones.
Backward pass. Otro método para calcular el gradiente (error asociado a los parámetros).
Gradiente descendente. En el tercer método implementaremos el gradiente descendente.
Entrenamiento. Durante la optimización vamos a monitorear el error global (otro método!) para verificar que el modelo vaya mejorando.

Antes de empezar con la implementación de la red, vamos a definir las funciones $\sigma(\cdot)$, $\sigma'(\cdot)$, y $softmax(\cdot)$. La función $softmax(\cdot)$ se encarga de normalizar la salida final del modelo de forma que cada neurona esté asociada a cierta probabilidad y que a la vez todas las neuronas de la capa de salida sumen a 1.

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def d_sigmoid(z):
    return (1 - sigmoid(z)) * sigmoid(z)

def softmax(z):
    exp_zi = np.exp(z)
    return exp_zi / np.sum(exp_zi, axis=1, keepdims=True)

Paso 1

Llamaremos a nuestra clase NeuralNet, y vamos a inicializar los parámetros aleatoriamente. Las dimensiones de nuestras matrices se podrán pasar por los argumentos del constructor. Además, vamos a tener un cache para almacenar los cálculos del “forward pass” que necesitaremos en el “backward pass”.

class NeuralNet:
    def __init__(self, input_dim=2, hidden_dim=5, output_dim=2):
        # Guardamos las dimensiones 
        self.inp_dim = input_dim
        self.hid_dim = hidden_dim
        self.out_dim = output_dim
        
        # Creamos la primera capa con valores aleatorios
        self.W1 = np.random.rand(self.inp_dim, self.hid_dim) / np.sqrt(self.inp_dim)
        self.b1 = np.zeros((1, self.hid_dim))
        
        # Creamos la segunda capa (la de salida)
        self.W2 = np.random.rand(self.hid_dim, self.out_dim) / np.sqrt(self.hid_dim)
        self.b2 = np.zeros((1, self.out_dim))
        
        # Un cache para facilitar el calculo en el "backward pass"
        self.cache = None

Paso 2

El “forward pass” es bastante simple. Tomamos la entrada x, la transformamos linealmente (z1) y la activamos (a1). Lo mismo hacemos con la segunda capa de la red utilizando la salida de la primera capa. El método retorna las predicciones del modelo.

    def forward(self, x):
        z1 = np.matmul(x, self.W1) + self.b1
        a1 = sigmoid(z1)

        z2 = np.matmul(a1, self.W2) + self.b2
        y_hat = softmax(z2)  # <-- softmax en lugar de sigmoid

        self.cache = {
            'a0': x,
            'z1': z1,
            'a1': a1,
            'z2': z2,
            'a2': y_hat
        }
        return y_hat

Nota que estamos utilizando softmax en lugar de sigmoid. De hecho, utilizar sigmoid sería más preciso para una tarea binaria; solo necesitamos una neurona para manejar dos clases. Sin embargo, queremos que este mismo código sea generalizable para tareas con más de dos clases, y la función softmax se encarga de manejar $n$ clases.

Otro detalle importante es que el cache contiene las transformaciones lineales (z’s) y las activaciones (a’s). Tanto la entrada $x$ como la salida $\hat{y}$ han sido estandarizadas con la misma nomenclatura. La idea es que este código pueda expandirse a una cantidad arbitraria de capas (tal como lo hicimos durante el taller 2).

Paso 3

Para la implementación de la función backward utilizaremos las derivadas que calculamos en la sección de propagación del error. Esta función solo recibe las clases reales por cada ejemplo en la entrada, y utiliza las transformaciones lineales y activaciones guardadas en el cache. El método retorna un diccionario con el resultado de las derivadas parciales del error con respecto a cada parámetro.

    def backward(self, y):
      """
      y: vector de forma (N,) con N samples y cada uno con un valor entre [0, C-1)
      """
      delta3 = np.copy(self.cache['a2'])  # y_hat -> la ultima activacion de la red
      delta3[range(len(y)), y] -= 1       # delta3 -> y_hat - y -> dL/dy_hat * dy_hat/dz2

      dW2 = np.matmul(self.cache['a1'].T, delta3)
      db2 = np.sum(delta3, axis=0)  # alternativamente: np.dot(np.ones((1, len(y))), delta3)

      delta2 = np.matmul(delta3, self.W2.T) * d_sigmoid(self.cache['z1'])
      dW1 = np.matmul(self.cache['a0'].T, delta2)
      db1 = np.sum(delta2, axis=0) 

      grad_dict = {
          'dW2': dW2,
          'db2': db2,
          'dW1': dW1,
          'db1': db1
      }
      return grad_dict

Es importante destacar que si hubiesen más capas, el proceso para calcular las derivadas se vuelve repetitivo. A excepción de la capa final (cuya derivada es $\hat{y} - y$), podríamos repetir el proceso $n$ veces. Como mencioné anteriormente, esto está en el código del segundo taller.

Paso 4

Ahora que ya tenemos listas las funciones de forward y backward podemos implementar el algoritmo del gradiente descendente. Para ello vamos a definir el método train que recibe como argumentos tanto la entrada $x$ como la salida esperada $y$. Además, el método recibe el radio de aprendizaje (learning rate, lr) para generar pequeños pasos al reducir el error. Es importante experimentar con este valor ya que un valor muy pequeño haría que el entrenamiento se alargue mucho, mientras que un valor muy grande podría hacernos diverger del mínimo local de la función de error que queremos alcanzar.

    def train(self, x, y, iters=200000, lr=0.01, verbose=True):
        # Gradiente descendente.
        for i in range(1, iters+1):
            # Correr el 'forward pass'
            probs = self.forward(x)

            # Colectar los gradientes del 'backward pass'
            grad_dict = self.backward(y)

            # Actualizar los parametros con el gradiente descendiente 
            # NOTA: necesitamos un pequeño paso negativo 
            self.W1 += -lr * grad_dict['dW1']
            self.b1 += -lr * grad_dict['db1']
            self.W2 += -lr * grad_dict['dW2']
            self.b2 += -lr * grad_dict['db2']

            if verbose and i % 1000 == 0:
                print("Error en la iteracion %i: %f" % (i, self.get_loss(probs, y)))

Cabe mencionar que la actualización de los parámetros se hace con la suma de un valor negativo. Como mencioné anteriormente, para minimizar el error tenemos que ir en la dirección opuesta al gradiente, de lo contrario estaríamos máximizando el error.

Paso 5

Las últimas dos líneas de la función de entrenamiento hacen que cada 1,000 iteraciones el modelo imprima el error global. De esta forma podemos monitorear si el modelo va mejorando o no. La función get_loss está implementada en base a la fórmula del error de “cross-entropy”.

    def get_loss(self, probs, y):
        N = len(y)  # N muestras
        C = len(set(y)) # C clases
    
        # Convertir el enumerado de clases en 'one-hot'
        one_hot = np.zeros((N, C)) # iniciamos el vector con ceros y dimensiones N x C
        one_hot[np.arange(N), y] = 1  # colocamos un uno solo en la clase adecuada

        # Cross entropy loss (negative log likelihood)
        loss = -np.sum(np.sum(np.multiply(one_hot, np.log(probs)), axis=1), axis=0)

        return (1. / N) * loss

Nota que la implementación de esta función es en base a $C$ clases, y no al caso específico de tareas binarias (dos clases). Por lo tanto, tenemos que convertir las clases $y$ en un vector “one-hot” y calcular el error solo en la clase definida por $y$.

Un vector “one-hot” es un vector de $C$ dimensiones, siendo $C$ el número de clases. Cada dimensión corresponde a una clase, y el vector solo contiene un uno en la dimensión de la clase determinada por $y$. El resto de sus valores son ceros.

Con estos pasos ya tenemos el código necesario para entrenar modelos en diferentes datos.

7. Moons dataset

El código completo para el modelo entrenado en el moons dataset está aquí

El moons dataset es un dataset de juguete que intercala dos semi círculos utilizando dos dimensiones ($x_1, x_2$). Cada semi círculo pertenece a una clase, y es posible agregar ruido a los puntos para hacer un tanto más real el escenario.

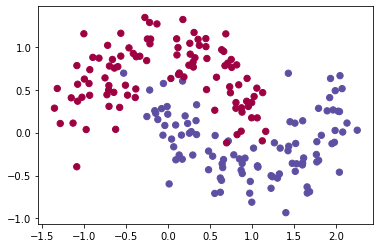
En la Figura 8 tenemos la visualización de 200 puntos del dataset. Los colores azul y rojo determinan las clases a la que pertenecen los puntos.

Con los detalles mencionados sobre el dataset, sabemos que

El número de elementos en la entrada es dos ($x_1, x_2$)
El número de elementos en la salida es dos ($y \in {0, 1}$).

Estos aspectos del dataset encajan perfectamente con las especificaciones del modelo en la Figura 7. Y ese es el modelo que vamos a instanciar y optimizar:

model = NeuralNet(input_dim=2, hidden_dim=5, output_dim=2)
model.train(x, y, iters=20000, lr=0.01)

> Error en la iteracion 1000: 0.151160
> Error en la iteracion 2000: 0.073622
> Error en la iteracion 3000: 0.064136
> Error en la iteracion 4000: 0.056121
> Error en la iteracion 5000: 0.050703
> Error en la iteracion 6000: 0.047125
> Error en la iteracion 7000: 0.044488
> Error en la iteracion 8000: 0.042473
> Error en la iteracion 9000: 0.040899
> Error en la iteracion 10000: 0.039640
> Error en la iteracion 11000: 0.038610
> Error en la iteracion 12000: 0.037748
> Error en la iteracion 13000: 0.037018
> Error en la iteracion 14000: 0.036396
> Error en la iteracion 15000: 0.035867
> Error en la iteracion 16000: 0.035421
> Error en la iteracion 17000: 0.035052
> Error en la iteracion 18000: 0.034754
> Error en la iteracion 19000: 0.034521
> Error en la iteracion 20000: 0.034342

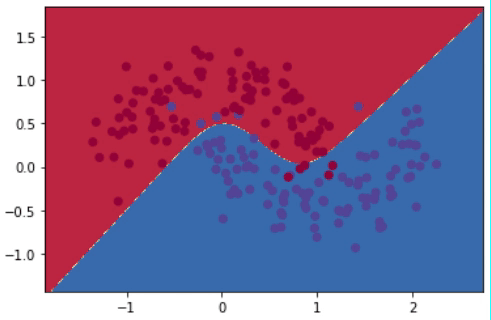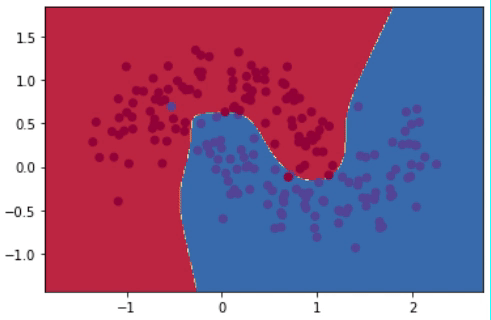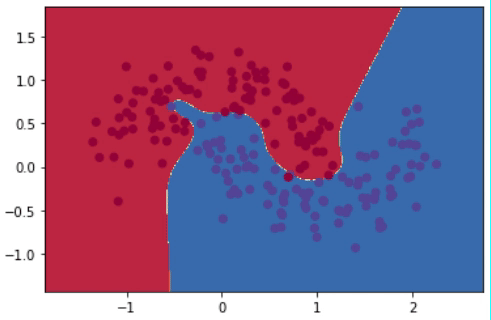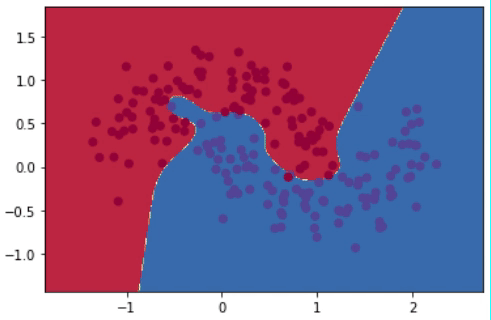
Después de realizar 20,000 iteraciones, el modelo logra reducir el error desde más de 0.15 hasta 0.03. El gif de la Figura 8 muestra la evolución del modelo cada 1,000 iteraciones. Se puede observar cómo el modelo va de una línea de decisión sencilla a una mucho más compleja y detallada.

Sin embargo, tener una línea que abarque todos los detalles perfectamente no es lo ideal. Esto se debe a que alguno de esos puntos podrían simplemente ser “outliers”, y no generalizables del compartamiento promedio de todos los puntos. Al capturar “outliers” se dice que estamos haciendo “overfitting”, es decir, el modelo está memorizando en lugar de generalizar. Entre las técnicas para prevenir overfitting están la regularización $\ell_2$ y el uso de dropout.

8. MNIST dataset

El código completo para el modelo entrenado en el MNIST dataset está aquí e incluye la abstracción de múltiples capas neuronales.

El segundo caso en el que evaluaremos nuestra red es en el MNIST dataset. Este dataset continiene imágenes de dígitos escritos a mano, y la tarea es determinar el digito en una imagen. Las imágenes son a blanco y negro y tienen una resolución de 28 x 28 pixeles.

Fig. 9 - Ejemplo del número ocho del MNIST dataset.

El dataset tiene un total de 70,000 imágenes. Este dataset contiene muchos más ejemplos que en el moons dataset, y es bastante más complejo.
Más específicamente, los nuevos retos con respecto al dataset anterior son:

El dataset es mucho más grande y colocarlo todo en memoria tomaría muchos recursos.
Las entradas son imágenes de 28x28 pixeles, es decir, 784 señales de entrada.
Tenemos que predecir 10 clases (10 digitos) en lugar de dos clases.

Considerando estos puntos, vamos a aprovechar que tenemos muchos más ejemplos para verificar que el modelo este generalizando en lugar de memorizando (overfitting).

Data de entrenamiento y evaluación

Nuestro primer paso va a ser dividir la data en dos partes, una de entrenamiento y otra de evaluación. La data de entrenamiento se ocupará para actualizar los parámetros como en el dataset anterior. Por el otro lado, La data de evaluación solo se utilizará para verificar que los resultados en la data de entrenamiento son consistentes y generalizables.

from sklearn.datasets import fetch_openml

def get_mnist_dataset():
    mnist = fetch_openml('mnist_784', version=1, cache=True)
    mnist.data = mnist.data / 255.
    mnist.target = mnist.target.astype(np.int8)
    return mnist
    
mnist = get_mnist_dataset()

x_train, x_test, y_train, y_test = \ 
    train_test_split(mnist.data, mnist.target, test_size=0.2, random_state=42)

Métrica de monitoreo

Para tener una mejor noción de cómo esta funcionando el modelo, vamos a monitorear una métrica de exactitud (“accuracy”). Esta métrica nos va a decir el porcentaje de números han sido predecidos correctamente en base al total de números evaluados. Si esta métrica es similar en entrenamiento y evaluación podemos asumir que el modelo está generalizando bien.

Batches y epochs

Adicionalmente, necesitamos incorporar el concepto de “batch” y “epoch”. Como no podemos procesar toda la data a la vez porque muy probablemente tendríamos problemas de recursos (“out-of-memmory exceptions”), vamos a dividir toda la data en pequeños segmentos, a los que llamamos batches. Al procesar todos los batches (toda la data) habremos completado un epoch. Es decir, entrenar por $n$ epochs es iterar por todo el dataset $n$ veces.

Con esto en mente, organizamos nuestro método de entrenamiento de la siguiente forma:

    def train(self, x, y, epochs=200, batch_size=32, lr=0.01):
        n_batches = epochs // batch_size 
        if epochs % batch_size != 0: 
            n_batches += 1

        for epoch in range(1, epochs+1):
            epoch_losses = []
            epoch_acc = []

            # Desordenar la data por cada epoch, para evitar que el   
            # modelo infiera a partir del orden en que le damos la data 
            x, y = shuffle(x, y)

            for batch_i in range(n_batches):
                x_batch = x[batch_size * batch_i: batch_size * (batch_i + 1)]
                y_batch = y[batch_size * batch_i: batch_size * (batch_i + 1)]

                # Correr el 'forward pass'
                probs_batch = self.forward(x_batch)

                # La actualización de parámetros es por cada batch de entrenamiento
                self.update_params(probs_batch, y_batch, lr)

                # Obtener el loss del batch actual
                loss = self.get_loss(probs_batch, y_batch)

                # Medir los resultados del modelo
                acc = accuracy_score(y_batch, np.argmax(probs_batch, axis=1))

                # Guardar los losses de todos los batches para hacer promedio al final del epoch
                epoch_losses += [loss] * len(x_batch)
                epoch_acc += [acc] * len(x_batch)

            print(f"Epoch {epoch} - Loss {np.mean(epoch_losses):.5f}, Accuracy: {np.mean(epoch_acc):.5f}")

    def update_params(self, probs, y, lr):
        # Colectar los gradientes 
        grad_dict = self.backward(y)

        # Actualizar los parametros con el gradiente descendiente (NOTA: es un pequeño paso negativo)
        self.W1 += -lr * grad_dict['dW1']
        self.b1 += -lr * grad_dict['db1']
        self.W2 += -lr * grad_dict['dW2']
        self.b2 += -lr * grad_dict['db2']

Entrenamiento

Con las nuevas modificaciones podemos echar a andar el modelo. Lo que haremos es entrenar por 200 epochs continuamente y luego evaluar el modelo en la data de test.

model = NeuralNet(input_dim=784, hidden_dim=256, output_dim=10)
model.train(x_train, y_train, epochs=200, batch_size=64, lr=0.01)

> Epoch 1 - Loss 18.05591, Accuracy: 0.10156
> Epoch 2 - Loss 17.80754, Accuracy: 0.08203
> Epoch 3 - Loss 4.31588, Accuracy: 0.11719
> Epoch 4 - Loss 2.97415, Accuracy: 0.14062
> Epoch 5 - Loss 2.56107, Accuracy: 0.14844
> Epoch 6 - Loss 2.48315, Accuracy: 0.15234
> Epoch 7 - Loss 2.36749, Accuracy: 0.16016
> Epoch 8 - Loss 2.38260, Accuracy: 0.15234
> Epoch 9 - Loss 2.27143, Accuracy: 0.19922
> Epoch 10 - Loss 2.31277, Accuracy: 0.18750
> ...
> Epoch 190 - Loss 0.25798, Accuracy: 0.92578
> Epoch 191 - Loss 0.38271, Accuracy: 0.86328
> Epoch 192 - Loss 0.37735, Accuracy: 0.89062
> Epoch 193 - Loss 0.32548, Accuracy: 0.90625
> Epoch 194 - Loss 0.32819, Accuracy: 0.90234
> Epoch 195 - Loss 0.28316, Accuracy: 0.92188
> Epoch 196 - Loss 0.27505, Accuracy: 0.92188
> Epoch 197 - Loss 0.28925, Accuracy: 0.92578
> Epoch 198 - Loss 0.32936, Accuracy: 0.90234
> Epoch 199 - Loss 0.25858, Accuracy: 0.94141
> Epoch 200 - Loss 0.28152, Accuracy: 0.91797

En el último epoch (aunque no el mejor) el modelo alcanzó 91.79% de accuracy en la data de entrenamiento. Ahora al correr el modelo en la data de evaluación esperamos tener un resultado similar:

y_hat_test = model.predict(x_test)
accuracy_score(y_test, y_hat_test)

> 0.9110714285714285

En efecto, obtenemos 91.10% de accuracy en la data de evaluación! Esto sugiere que el modelo es capaz de reconocer números que no ha visto antes y de mantener más o menos la misma exactitud.

9. Conclusión

En este post cubrimos los componentes básicos de redes neuronales artificiales. A partir de discutir la teoría y dar motivación del porqué de cada componente, implementamos nuestra versión de una red neuronal. Luego probamos la red en dos datasets: Moons dataset y MNIST dataset.

Este post es la versión escrita del taller 1 que conduje en la comunidad de Data Science El Salvador. Si te interesan estos temas, puedes unirte a la comunidad en su página en Facebook o LinkedIn.

Cualquier duda, pregunta, corrección o comentario es bienvenido!

Agradecimientos

El contenido mostrado en este post ha sido creado a partir de mis notas de estudio en diferentes lugares y cursos a lo largo de mi doctorado. Las prinicipales fuentes son:

Fundamentals of Machine Learning (Rice University)
Advanced Natural Language Processing (University of Houston)
Machine Learning (Coursera)
Deep Learning Nanodegree (Udacity)